Post-Quantum Now: From AES & RSA to ML-KEM Hybrids
October 3, 2025
10 min read
The Digital Trust Infrastructure: Foundations of Modern Encryption
In modern systems, encryption isn’t monolithic. It’s an orchestration of specialized components that each fulfill a different security function. These systems are designed with modularity in mind, enabling flexibility and long-term maintainability.
Symmetric cryptography, such as AES, is used for bulk data encryption because it is fast and efficient. This type of cryptography uses the same key for both encryption and decryption, making it ideal for protecting high-throughput or stored data.
Asymmetric cryptography, including RSA and elliptic curve algorithms like ECDH (Elliptic Curve Diffie-Hellman), is used primarily for key exchange and digital signatures. It enables parties who have never met before to securely exchange cryptographic keys over an insecure network.
Hash functions like SHA-256 ensure data integrity and feed into Key Derivation Functions (KDFs) like HKDF. These derive strong keys from a shared secret, often combining context information or transcript data to avoid key reuse or collision between sessions. Below you can see HKDF key derivation example:
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives import hashes
def derive_key(secret, info):
return HKDF(
algorithm=hashes.SHA256(),
length=32,
salt=None,
info=info
).derive(secret)This snippet derives a 32-byte session key from a shared secret using HKDF(SHA-256), binding it to the current session via info (e.g., a handshake transcript); salt=None here is for demo — use a fixed, versioned salt in production.
As an example of the modularity and complexity of the architecture of modern cryptosystems, let us consider a TLS-style session:
The client and server exchange public keys (e.g., X25519 or RSA).
Each side calculates a shared secret (e.g., via ECDH or KEM).
A KDF consumes the shared secret and the full handshake transcript (including version, parameters, public keys, etc.) to derive session keys.
These session keys are used with an authenticated encryption mode (like AES-GCM) to encrypt all subsequent traffic.
This layered model enables crypto agility—you can update a key exchange algorithm (e.g., move from ECDH to ML-KEM) without rewriting the entire protocol stack or re-encrypting stored data. It also supports forward secrecy, ensuring that compromise of long-term keys doesn’t expose past sessions.
AES — The Workhorse of Confidentiality
AES (Advanced Encryption Standard) is a symmetric block cipher standardized by NIST in 2001. It operates on fixed-size 128-bit blocks and supports key lengths of 128, 192, or 256 bits. Internally, AES consists of multiple rounds of transformations: SubBytes (non-linear substitution), ShiftRows (permutation), MixColumns (linear mixing), and AddRoundKey (XOR with the round key). These rounds provide strong confusion and diffusion, making AES resistant to differential and linear cryptanalysis. You can read more about this algorithm in the relevant standard.
AES is widely trusted due to its simplicity, efficiency, and the availability of hardware acceleration through AES-NI (on x86 CPUs) and ARMv8 cryptographic extensions. It forms the backbone of many secure systems, including disk encryption, VPNs, messaging apps, and TLS.
Let’s break down the essential internal steps for AES-128:
10 rounds for AES-128, each round includes SubBytes → ShiftRows → MixColumns → AddRoundKey
Final round omits MixColumns
Uses Rijndael’s key schedule to expand keys
Textual AES Illustration:
Plaintext: 6bc1bee22e409f96e93d7e117393172a
Key: 2b7e151628aed2a6abf7158809cf4f3c
Ciphertext: 3ad77bb40d7a3660a89ecaf32466ef97You can verify this using libraries like OpenSSL or Python’s cryptography module.
Choosing the Right AES Mode
AES-GCM (Galois/Counter Mode). Offers both confidentiality and integrity (AEAD). It’s the standard in TLS 1.3, QUIC, IPsec, and many secure messaging systems. However, it is fragile with nonces. If you repeat a nonce with the same key, attackers can recover plaintexts and authentication keys.
AES-SIV (Synthetic IV). Designed for scenarios where enforcing nonce uniqueness is difficult. It is misuse-resistant, meaning even if nonces repeat, security is not catastrophically broken. It’s slower but a better default for embedded or multi-tenant systems where nonce coordination is risky.
AES-XTS (XEX-based Tweaked CodeBook mode with ciphertext stealing). Used for disk encryption. It ensures that even if the same block appears twice (e.g., empty sectors), it gets encrypted differently. Not safe for general-purpose AEAD use.
Key Size and Post-Quantum Considerations
AES is considered quantum-resistant when used with longer key sizes. While Grover’s algorithm gives a quadratic speedup for brute-force attacks, using AES-256 maintains a high security margin even in the face of future quantum hardware.
Nonce Management: The Achilles’ Heel of GCM
In AES-GCM, the nonce must never repeat for a given key. Reuse can lead to loss of confidentiality and forgery of messages. This makes nonce management critical:
Use 96-bit (12-byte) random or counter-based nonces.
In distributed systems, pre-allocate nonce ranges to different nodes or use hybrid schemes (e.g., prefix + counter).
If you can’t guarantee uniqueness, switch to AES-SIV.
AES-GCM Example:
from cryptography.hazmat.primitives.ciphers.aead import AESGCM
import os
key = AESGCM.generate_key(bit_length=256)
aead = AESGCM(key)
nonce = os.urandom(12) # Must be unique per key
aad = b"ctx:app|ver=1|tenant=acme"
plaintext = b"secret data"
ciphertext = aead.encrypt(nonce, plaintext, aad)
decrypted = aead.decrypt(nonce, ciphertext, aad)Use AAD to bind context — like purpose, version, or tenant ID — to the ciphertext, reducing risk of cross-context replay.
The Storm on the Horizon: The Quantum Threat
Quantum computers, once sufficiently mature, will break much of the public-key cryptography we use today. Shor’s algorithm allows factoring of large integers and computation of discrete logarithms in polynomial time, meaning RSA, DSA, and ECDSA will no longer be secure.
Grover’s algorithm, on the other hand, offers a quadratic speedup for brute-force attacks against symmetric ciphers. This means AES-128 offers only 64 bits of post-quantum security, so AES-256 is preferred.
Harvest Now, Decrypt Later (HNDL): This refers to adversaries collecting encrypted communications now, with the expectation that future quantum computers will allow them to decrypt it later. This is particularly critical for industries where confidentiality must last 5–10+ years.
This impacts: medical archives, legal documents, financial data—anything requiring secrecy for years.
Forging a New Shield: The Rise of Post-Quantum Cryptography
To defend against quantum attacks, new cryptographic schemes have emerged that rely on hard mathematical problems that even quantum computers can’t efficiently solve. These problems include lattice-based constructions, code-based encryption, multivariate polynomials, and hash-based signatures.
The National Institute of Standards and Technology (NIST) has led a global competition to evaluate and standardize such algorithms. After several years of cryptanalysis and community feedback, NIST has announced its first set of recommended post-quantum algorithms:
ML-KEM (Kyber): Kyber is a Key Encapsulation Mechanism based on the Module-LWE (Learning With Errors) problem. It works by creating a ’noisy’ linear system using matrix-vector operations over polynomials. The security comes from the difficulty of recovering secrets from these noisy structures. Kyber is chosen because it offers a balance of performance, size, and security.
How Kyber Works:
The receiver generates a secret polynomial and a public matrix.
The sender encrypts a random key using the receiver’s public key (adding noise).
The receiver uses their secret to remove the noise and recover the shared key.
Textual Example:
Kyber ciphertext: 0x01a2... (compressed polynomial vectors)
Shared secret: b"..."ML-DSA (Dilithium): This is a lattice-based digital signature algorithm. It relies on rejection sampling to ensure that signatures do not leak information about the secret key. Dilithium’s efficiency and conservative design make it ideal for use in future PKIs.
How Dilithium Works:
The signer hashes the message to create a challenge.
A pseudo-random commitment is generated.
The challenge and secret key produce a response.
The verifier checks this response against the commitment and challenge.
Signature Example:
Message: "auth=login"
Signature: 0x43a9... (polynomial coefficients)
Verified: TrueClassical vs Post-Quantum Algorithms at a Glance
| Algorithm | Type | Security Basis | Quantum-Safe | Key Size | Signature Size | Performance |
|---|---|---|---|---|---|---|
| RSA-2048 | Encryption / Signature | Integer Factorization | ❌ | ~256 bytes | ~256 bytes | Moderate |
| X25519 | Key Exchange | Elliptic Curves | ❌ | 32 bytes | — | High |
| Kyber-768 | Key Encapsulation (KEM) | Lattices (MLWE) | ✅ | ~1,184 bytes (pub) | — | Fast |
| Dilithium-2 | Digital Signature | Lattices (MLWE/MPLWE) | ✅ | ~1,300 bytes (pub) | ~2,420 bytes | Efficient, Medium size |
Classical vs Post-Quantum: Performance Snapshot
While classical algorithms like X25519 and RSA-2048 are deeply optimized and fast for most applications, post-quantum schemes introduce trade-offs between security and efficiency:
- Kyber offers high-speed key exchanges, even outperforming RSA in many scenarios. It’s suitable for TLS handshakes and IoT due to its small ciphertext and fast computation.
- Dilithium, though secure and well-designed, has larger signature sizes and moderate verification speed. It’s efficient enough for most PKI systems but might require optimization on constrained devices.
- X25519 remains extremely lightweight, making it ideal for mobile and embedded systems—but it offers no quantum resistance.
In practice, performance is no longer just about speed — it must also account for resilience to quantum threats.
The National Institute of Standards and Technology (NIST) has led a global competition to evaluate and standardize such algorithms. After several years of cryptanalysis and community feedback, NIST has announced its first set of recommended post-quantum algorithms:
ML-KEM (Kyber): A lattice-based Key Encapsulation Mechanism (KEM) used for establishing shared secrets. It’s fast, compact, and relatively easy to implement, making it ideal for replacing ECDH in many systems.
ML-DSA (Dilithium): A lattice-based digital signature algorithm that can serve as a future-proof alternative to RSA and ECDSA. It is also efficient, but signature sizes are larger compared to traditional schemes.
These algorithms have been implemented in several well-maintained libraries, such as:
liboqs: C library with wrappers for many post-quantum algorithms, including ML-KEM and ML-DSA.
PQClean: A collection of clean and portable implementations in plain C.
pyoqs: Python bindings to liboqs, allowing easy experimentation in Python environments.
The transition to PQC doesn’t mean discarding current crypto overnight. Instead, a gradual adoption path using hybrid systems (classical + post-quantum) allows you to maintain interoperability while preparing for quantum threats.
Ultimately, the rise of post-quantum cryptography is about resilience: securing long-lived data, protecting critical infrastructure, and ensuring privacy in a world where quantum computing is no longer theoretical but inevitable.
A Practical Deep Dive: Implementing a Kyber-Based Hybrid System
The recommended approach today is hybrid key exchange:
Combine a classical key exchange (X25519) with ML-KEM.
Derive the final session key from both shared secrets.
Bind this key to the handshake transcript.
This gives you forward secrecy (X25519) and quantum resilience (ML-KEM).
Hybrid Key Derivation Function:
import hashlib
def derive_hybrid_key(ecdh_secret, pq_secret, transcript):
combined = ecdh_secret + pq_secret
info = b"hybrid-v1|" + hashlib.sha256(transcript).digest()
return derive_key(combined, info)This script combines the classical ECDH secret and the post-quantum KEM secret, then derives a 32-byte session key via HKDF with a versioned, transcript-bound info string — this binds the key to the handshake and thwarts downgrade/context mix-ups.
Hybrid Session Example (using pyoqs):
from cryptography.hazmat.primitives.asymmetric import x25519
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives import hashes
import oqs, hashlib
# Server side (PQ)
srv_kem = oqs.KeyEncapsulation("Kyber768")
srv_pub = srv_kem.generate_keypair() # keep srv_kem for decapsulation
# Client side
clt_x = x25519.X25519PrivateKey.generate()
srv_x = x25519.X25519PrivateKey.generate() # demo only; it's server key in real systems
shared_ecdh = clt_x.exchange(srv_x.public_key())
clt_kem = oqs.KeyEncapsulation("Kyber768", srv_pub)
ct, clt_shared = clt_kem.encap_secret()
# Server side decapsulation
srv_shared = srv_kem.decap_secret(ct)
assert clt_shared == srv_shared
# Transcript binding
transcript = b"|".join([
b"tls13",
b"x25519", srv_x.public_key().public_bytes_raw(),
b"kyber768", srv_pub
])
def derive_hybrid_key(ecdh_secret, pq_secret, transcript, salt=b"hybrid-salt-v1"):
info = b"hybrid-v1|" + hashlib.sha256(transcript).digest()
return HKDF(algorithm=hashes.SHA256(), length=32, salt=salt, info=info).derive(ecdh_secret + pq_secret)
session_key = derive_hybrid_key(shared_ecdh, clt_shared, transcript)This key can now be used in an AEAD (e.g., AES-GCM) for secure communication.
The Path Forward: Migration Roadmap & Crypto Agility
The transition to post-quantum cryptography must be both strategic and gradual. PQC algorithms are new, and real-world deployment brings new complexities. An effective rollout requires observation, measurement, policy controls, and fallback plans.
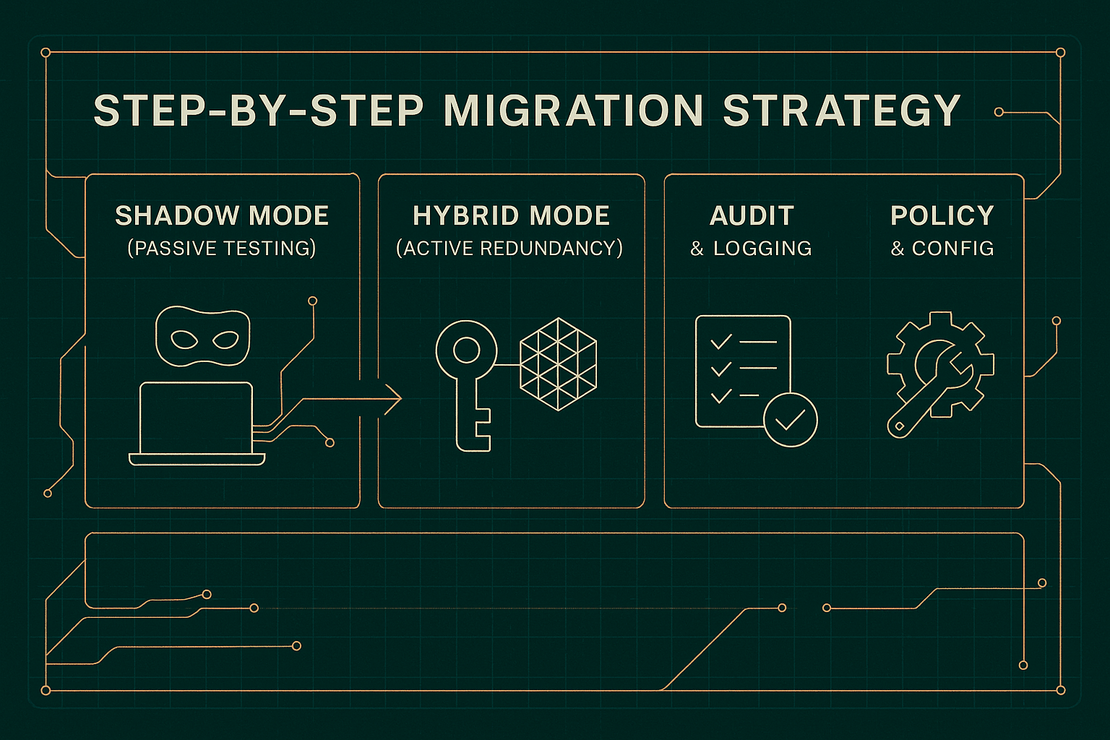
Step-by-Step Migration Strategy
Shadow Mode (Passive Testing). Deploy PQC algorithms like ML-KEM alongside existing key exchanges, but don’t use them to derive session keys yet. Instead, log performance, message sizes, failure rates, and client support. This phase builds operational confidence without risking compatibility.
Hybrid Mode (Active Redundancy). Introduce hybrid key exchanges: derive a session key from both classical and post-quantum secrets. Only accept the connection if both succeed. This ensures security today (via X25519) and in the quantum future (via ML-KEM).
Audit, Logging & Visibility. Record every handshake’s outcome, the selected ciphersuites, handshake times, failures, and version metadata. This data allows for debugging, rollback, and compliance.
Policy & Config. Control teams must be able to toggle PQ algorithms via configuration. Apply feature flags per customer, region, or environment. You’ll need different rollout speeds for internal services vs. external APIs.
Crypto Agility Best Practices
Configurable Ciphersuites: Avoid hardcoding algorithms. Load them via configuration files or environment variables.
Versioned Derivation Labels: Example — use b"hybrid-v1" for HKDF info fields. When you upgrade formats or algorithms, increment the version.
Frequent Key Rotation: Don’t treat PQC keys as static. Rotate ML-KEM public keys on a schedule. Rotate AES keys tied to those secrets too.
Downgrade Detection: Use the transcript hash to detect missing PQ elements in hybrid mode. Log or alert on unexpected algorithm falls.
Rollback Drills: Simulate failure of PQ components. Make sure your system can fall back to classical crypto or alternate KEMs gracefully.
Conclusion: Securing the Post-Quantum Future Today
Quantum computing is no longer a distant possibility — it’s a developing reality that will disrupt the foundations of digital security. Current cryptographic protocols, especially those based on RSA and elliptic curves, will become vulnerable once sufficiently large quantum computers emerge. The implications span industries: healthcare, finance, national defense, intellectual property, and critical infrastructure all depend on long-term confidentiality.
But here’s the good news: we don’t need to wait for quantum to act. The cryptographic community has anticipated this transition. Tools, libraries, and standards are already available for post-quantum readiness.
Here’s what you can — and should — do now:
- Keep AES, especially with 256-bit keys. It’s resilient to quantum attacks and widely supported.
- Continue using X25519 or other well-established classical curves, but pair them with post-quantum algorithms.
- Deploy ML-KEM (Kyber) as part of a hybrid key exchange strategy. It offers efficient, quantum-safe key establishment.
- Bind derived keys to handshake transcripts, preventing context drift and enforcing strict cryptographic hygiene.
Post-quantum hybrid systems offer the best of both worlds: they’re secure against today’s threats while preparing for tomorrow’s. Once PQ digital signature schemes like ML-DSA (Dilithium) are integrated into your PKI and hardware ecosystem (e.g., HSMs, tokens, secure elements), you’ll be ready to phase out vulnerable primitives entirely.
This is not just a technical shift — it’s a shift in mindset. Security engineering must now embrace:
- Versioning of cryptographic decisions
- Audit trails and rollback procedures
- Ongoing testing and cryptographic agility
Start where the stakes are highest—systems with long-lived secrets, regulated compliance requirements, or persistent threat models. Begin by observing, then layering PQC in shadow mode, and ultimately enforcing it across environments.
Post-quantum security isn’t just about being safe in 10 years. It’s about staying trustworthy today.
Related Posts

August 13, 2025
Bug Bounty 101: The Best Courses to Get Started in 2025

July 25, 2025
The Pyramid of Pain: Beyond the Basics

June 14, 2025
Domain Recon: Must-Know Tools for Security Professionals

September 12, 2025
Bug Bounty 101: Top 10 Reconnaissance Tools

August 8, 2025
I, Robot + NIST AI RMF = Complete Guide on Preventing Robot Rebellion

July 7, 2025
DNS Cache Poisoning – Is It Still Relevant?